Legend of the calendar of the cumulative-dissipative cycle in seeds.

Contents:

1 - Premises.
2 - The sidereal month.
3 - The calendar.
4 - What the calendar is for.
5 - Variation of the declination of the Moon and its effects.
Auxiliary informations.

- 1 -

Premises.

The angular velocity of the Moon around the Earth varies, inducing in seeds the cumulative dissipative cycle, thanks to which they maintain their viability for a long time.

To facilitate the reading of the calendar of the cumulative-dissipative cycle of the seeds, it does not indicate the angular velocities of the seeds relative to the Moon, but indicates how much, every day, the Moon proceeds in its journey around the Earth.

The calendar is useful also in the research on tides.

- 2 -

The sidereal month.

Bear in mind that the Moon completes its rotation around the Earth in 27 days, 7 hours, 43 minutes, 12 seconds (sidereal month).

The time of the sidereal month is subdivided by me into 86.400 deltins, a unit of measure I use in the graphs of the calendar of the cumulative-dissipative cycle of the seeds, at rest on the ground.

The number of 86,400 deltins is the same number of the seconds as there are in 24 hours. However, the two words, second and deltin, indicate different meanings and durations.

The calendar indicates how the total of 86400 deltins is distributed over the various days of the sidereal month.

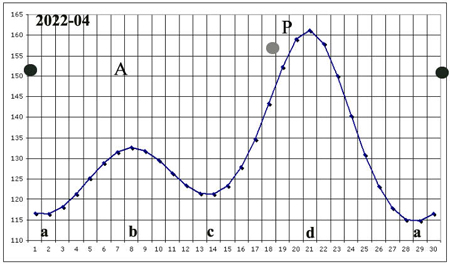
In the graphs of this calendar, the angular velocities of the Moon around the Earth are shown, expressed in deltins, either for each day of the sidereal month, or as an hourly average of each day, as in the two examples below.

Monthly calendar.

We can see this variation in angular velocity over the course of a month, in the calendar below. The grid of the days is in accordance with the universal time (GMT).

cumulative dissipative cycle of the seeds

The angular velocity, given as hourly average per each day, of how much the Moon recovers its delay, on its revolution around the Earth, defined in 86400 deltins, and performed during one sidereal month.

What the calendar is for.

1 - It indicates the phases of the cycle of the seeds.

As far for the seeds, the calendar shows when they are in the cumulative phase (periods b-c; d-a), and when they are in the dissipative phase (periods a-b; c-d).

2 - It indicates how much angular velocity varies.

The calendar also gives an idea of the efficiency of the cycle.

Indeed, the cumulative-dissipative processes in the seeds take place only at critical values of angular velocity, relative to the Moon, and therefore only during brief episodes of interaction.

The less the angular velocity of the Moon, relative to the Earth, varies, the longer the episodes of interaction, the more numerous and efficient the cycle processes, ceteris paribus.

3 - Critical discrete values.

To date, the critical discrete values of angular velocity, valid for the seeds, are exploited at random, since they are still undefined. I am alone, and not engaged in this part of the research, because it would require a team, knowledge and facilities that I do not have.

4 - Zero variation.

The calendar is also useful in tidal research, because it indicates when the angular velocity of the Moon around the Earth does not vary. It is then that it is possible to identify the critical angular velocities of the Moon, around the Earth, valid for water, when the episodes of interaction, at a given critical angular velocity, are long, and the phenomenon of the formation of the tide, Understood as decrease of the density of the water, it becomes evident, thanks to the formation of water protuberances, or of "density waves".

- 5 -

The range of variation of the declination of the Moon.

In each page of the calendar, just under the number of the month, you may see the two extremes of the declination of the Moon, relative to the equator (example: N 21 00 decl. S 21 00).

The larger the range, the more the values of angular velocity per unit of time vary, the less probable the seeds will complete the recovering of viability, at each cycle, ceteris paribus, with unfavourable implications for the productivity of the plants, grown from seeds germinated at that time.